Das Problem des Handlungsreisenden (engl. „Traveling Salesman Problem“) ist ein kombinatorisches Optimierungsproblem und gehört zur Klasse der NP-vollständigen Probleme der Mathematik. Auf deutsch: Schwere Kost.

Das Problem

Stell dir vor, du bist Paketzusteller bei einem Versandhändler. Während deines Arbeitstages musst du eine bestimmte Zahl von Paketen an Kunden in deiner Stadt liefern. Nun wohnen jedoch nicht alle Kunden in einer Straße, sondern verstreut in der ganzen Stadt. Du willst nicht mehr Zeit als nötig auf Reisen verbringen und deinen Kunden so schnell wie möglich die Ware liefern. Wie solltest du dann am besten deine Route planen? Du startest mit deinem Lieferwagen von zu Hause und willst dort auch wieder ankommen. Für den Rest der Route bleibt dir aber ein großer Spielraum. Wie groß ist dieser?

Doch so klein

Gut, dass du fragst! Fangen wir ganz klein an. Bei einem Kunden ist klar, wie man seine Reise plant. Einmal hin und einmal zurück. Bei zwei Kunden hat man die Wahl, Kunde 1 oder Kunde 2 zuerst zu besuchen, und dann jeweils den anderen. Bei drei Kunden haben wir hingegen schon 6 Möglichkeiten:

[Kunde 1 -> Kunde 2 -> Kunde 3]

[Kunde 1 -> Kunde 3 -> Kunde 2]

[Kunde 2 -> Kunde 3 -> Kunde 1]

[Kunde 2 -> Kunde 1 -> Kunde 3]

[Kunde 3 -> Kunde 1 -> Kunde 2]

[Kunde 3 -> Kunde 2 -> Kunde 1]

Bei vier Kunden gibt es 12 mögliche Routen, bei fünf Kunden sind es 60 mögliche Routen. Die Anzahl der möglichen Reisewege wächst nicht proportional zur Kundenzahl, sondern viel stärker. Genauer: Wenn „n“ die Kundenzahl ist, dann ist die Anzahl der möglichen Routen „n!“ (n Fakultät).

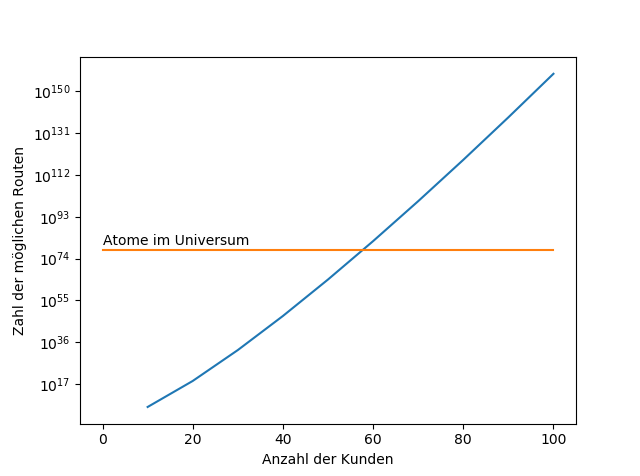
Du willst 60 Kunden persönlich besuchen? Glückwunsch! Bei der Wahl deiner Reiseroute stehen dir nur knapp mehr Möglichkeiten zur Verfügung als es Atome im Universum gibt. Also alles halb so schlimm. Außerdem: Da dir egal ist, ob du eine Rundreise „vorn“ startest oder diese in umgekehrter Reihenfolge hinter dich bringst, fällt noch mal die Hälfte aller Möglichkeiten weg. Sind dann leider immer noch mehr Optionen als Atome im Universum.

Nah am Alltag

Es gibt mathematische Probleme, die den meisten weit hergeholt vorkommen. Dieses Problem kann man jedoch leicht in den Alltag einbetten. Wie plant der Bote des Online-Versandhauses deiner Wahl seine tägliche Route, um so viele Pakete wie möglich zuzustellen? Wie planen Fluggesellschaften ihre Routen, um so wenig Treibstoff wie möglich zu verbrauchen? Wie kann der Weihnachtsmann an einem Abend Millionen von Haushalten auf der ganzen Welt Geschenke bringen?

Falls du mehr über das Problem des Handlungsreisenden und mögliche Lösungen wissen willst: Wikipedia.