Wie versprochen widmen wir uns jetzt den Unterschieden zwischen den Wohnungen der einzelnen Bundesländer und arbeiten in diesem Zusammenhang mit einer weiteren Methode der Visualisierung, nämlich Boxplots.

Was ist ein Boxplot?

Boxplots sind oft Teil der explorativen Datenanalyse (EDA) und liefern einen Einblick in die Verteilung einer Reihe von Daten. Gucken wir uns dazu mal ein Beispiel an.

Der Boxplot oben zeigt die Verteilung der Kaltmieten nach Bundesländern. Doch was genau bedeutet „Verteilung“ in diesem Zusammenhang? Beginnen wir mit den schwarzen Strichen innerhalb der Boxen. Diese zeigen den Median, das Zentrum der Daten. Schauen wir uns zum Beispiel die bayrischen Wohnungen an, von denen es im Datensatz 6.512 gibt. Jetzt sortieren wir die Kaltmieten dieser Wohnungen aufsteigend. Der Median ist dann der Durchschnitt aus der 3256. und der 3257. Kaltmiete, also aus den mittleren zwei Merkmalsausprägungen. Bei einer ungeraden Anzahl ist der Median genau die mittlere Ausprägung. In Bayern beträgt dieser Median 680€, in Sachsen-Anhalt hingegen 326€. Eine praktische Eigenschaft des Medians ist seine Resistenz gegenüber Ausreißern. Selbst wenn zum Beispiel die oberen 10% der Wohnungen in Bayern doppelt so teuer wären, würde der Median immer noch derselbe bleiben.

Die Boxen, welche auch den Median einschließen, umfassen genau die mittleren 50% der Daten. Sowohl das untere als auch das obere Viertel der sortierten Daten liegt also außerhalb der Boxen. So kann man einschätzen, ob die Ausprägungen eher dicht beieinander liegen oder breit gestreut sind. In Bayern erstreckt sich die mittlere Hälfte der Kaltmieten von 480€ bis 990€, in Nordrhein-Westfalen von 350€ bis 650€. Beim Vergleich dieser zwei Bundesländer sieht man nicht nur, dass Wohnungen in Bayern im Mittel teurer sind, sondern auch, dass hier die Kaltmieten breiter gestreut sind als in Nordrhein-Westfalen.

Und dann gibt es da noch diese von den Boxen ausgehenden Linien, auch „Whiskers“ (engl. für „Schnurrhaare“) genannt. Für die Länge der Whiskers gibt es unterschiedliche Berechnungen. Die am häufigsten genutzte ist der mit einem Faktor von 1,5 multiplizierte Interquartilsabstand (IQR) – der Abstand zwischen dem oberen und dem unteren Rand der Box. Dieser beträgt in Bayern 510€. Mit 1,5 multipliziert haben wir 765€. Also erstreckt sich der obere Whisker theoretisch vom Rand der Box bis zum Wert von 990€ + 765€ = 1755€. Allerdings hört der Whisker bei der letzten Merkmalsausprägung auf, die noch innerhalb der 1,5-fachen IQR liegt. Wenn die letzte Wohnung mit einer Kaltmiete kleiner oder gleich 1755€ nur 1700€ kostet, dann hört der Whisker hier auf. Analog dazu verfährt man mit dem unteren Whisker.

Weitere Beispiele

Jetzt, wo wir uns mit Boxplots vertraut gemacht haben, können wir weitere Eigenschaften des Datensatzes mit ihrer Hilfe inspizieren.

Anscheinend sind die Wohnungen in den neuen Bundesländern nicht nur die günstigsten, sondern auch die kleinsten. Wie im Boxplot oben erreichen auch hier manche Whisker die Nulllinie. Einige Wohnungen haben laut ImmobilienScout24 also eine Wohnfläche von 0 Quadratmetern. Kuschelig… zum Glück sind die Dimensionen der Boxen diesen Ausreißern gegenüber resistent.

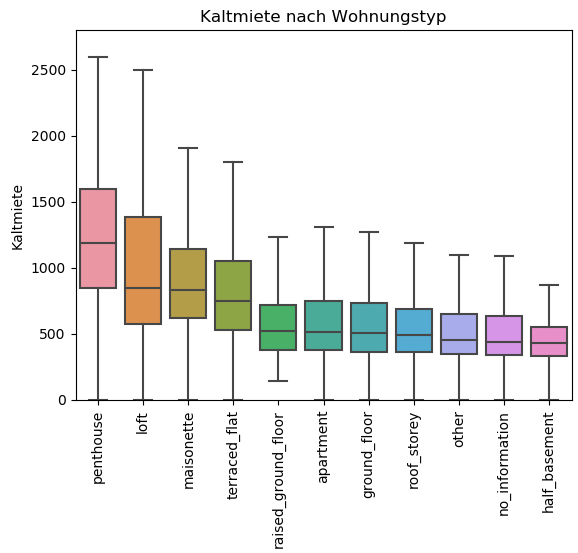
Hier haben wir die Verteilung der Kaltmieten, gruppiert nach Wohnungstyp. Wie zu vermuten war, sind Penthäuser am teuersten. Hier liegen die mittleren 50% der Mieten zwischen 850€ und 1.600€. Bei Wohnungen im Souterrain liegen diese dagegen zwischen 330€ und 550€. Einer der Gründe für den hohen Preis bei Penthouse-Wohnungen ist die Wohnfläche.

Die mittlere Wohnfläche von Penthäusern ist mehr als doppelt so groß wie die mittlere Wohnfläche von Souterrain-Wohnungen. Das erklärt so einiges.

Jetzt, wo wir Boxplots kennengelernt haben, können wir uns im nächsten Beitrag einer weiteren Art der Datenvisualisierung widmen.