ImmobilienScout24 Mining Teil 4.1: Beginn der EDA in Python
Was ist EDA?
EDA (Explorative Datenanalyse) bedeutet, sich einen Überblick über einen Datensatz zu verschaffen und ein Gefühl für die Daten zu bekommen. Hier werden noch keine Annahmen darüber getroffen, wie welche Variablen verteilt sind oder mit welchen statistischen Modellen die Auswirkungen eines Merkmals auf ein anderes Merkmal erklärt werden können. Man spielt mit den Daten und gewinnt erste Einblicke. EDA ist also der Beginn jeder fundierten Analyse.
Ein grober Überblick und erste Hürden
Nachdem wir im letzten Artikel die Daten grundlegend gesäubert haben, können wir uns jetzt mit den Inhalten beschäftigen. Zuerst müssen wieder die benötigten Packages importiert werden.
import pandas as pd import matplotlib.pyplot as plt
Gucken wir uns erst mal an, wo sich die Wohnungen befinden, die der Scraper heruntergeladen hat.
df.geo_bln.value_counts(normalize=True).plot(kind="bar")
plt.ylabel("Relative Häufigkeit")
plt.xlabel("Bundesländer")
plt.show()

Mehr als ein Viertel der Wohnungen kommen aus Nordrhein-Westfalen. Der Anteil der Wohnungen aus dieser Region ist noch größer als der Anteil der dort wohnenden Menschen an Deutschlands Gesamtbevölkerung. Man könnte die Hypothese aufstellen, dass dort entweder relativ viel neu gebaut wird oder die Mieterfluktuation einfach höher als woanders ist. Wie sieht es mit der Verteilung der Kaltmieten aus?
plt.hist(df.obj_baseRent) plt.show()

Schon jetzt stoßen wir auf ein Problem, mit dem jeder Analyst zu kämpfen hat: Ausreißer. Anscheinend liegt bei einer oder mehreren wenigen Wohnungen die Kaltmiete bei rund 10 Mio. Euro. Das schauen wir uns genauer an.
df.obj_baseRent.max()
10000000.0
Tatsächlich. Bei dieser Kaltmiete kann es sich eigentlich nur um einen Fehler handeln. Gucken wir uns trotzdem mal ein paar mehr Merkmale dieser Wohnung an. Dazu schauen wir, in welcher Zeile des Datensatzes sich die Wohnung befindet.
df.obj_baseRent.argmax()
38978
Die Funktion .argmax() gibt gibt den Wert des Index zurück, an dem sich der größte Wert eines Arrays befindet. Jetz kennen wir also die Stelle, an der sich die Wohnung befindet, und können sie genauer inspizieren.
df.iloc[38978,:][["beschreibung", "geo_bln", "geo_krs",
"geo_plz", "obj_balcony", "obj_cellar",
"obj_condition", "obj_floor", "obj_garden",
"obj_hasKitchen", "obj_heatingType",
"obj_interiorQual", "obj_lastRefurbish",
"obj_lift", "obj_livingSpace",
"obj_newlyConst", "obj_noParkSpaces",
"obj_noRooms", "obj_totalRent",
"obj_typeOfFlat", "obj_yearConstructed"]]

Die Wohnung befindet sich in Köln, hat ein Zimmer, liegt im 5. Stock und hat 75qm. Kein Garten, kein Balkon, keine Einbauküche, kein Neubau, kein Keller, kein Aufzug. Keine Informationen über das Baujahr, den Zustand oder das Jahr der letzten Renovierung. Da die Wohnung auf der Seite von ImmobilienScout24 nicht mehr zu finden ist, lässt sich die Kaltmiete auch nicht korrigieren. Und weil die Wahrscheinlichkeit, dass eine Wohnung wirklich 10 Mio. Euro im Monat kostet, verschwindend gering ist, lösche ich die Wohnung aus dem Datensatz. Oder nicht? Was ist, wenn danach die teuerste Wohnung 9 Millionen Euro pro Monat kostet? Vielleicht sitzen wir noch den ganzen Tag hier und löschen manuell die teuersten Wohnungen. Wir können uns ja mal die Kaltmieten der 20 teuersten Wohnungen anschauen.
df.obj_baseRent.sort_values(ascending=False)[:20].plot(kind="bar") plt.show()

Es gibt also nur wenige extreme Ausreißer nach oben. Wie sieht es auf der anderen Seite aus?
df.obj_baseRent.min()
0.0
Die niedrigste Kaltmiete beträgt 0€. Nicht gut. Gibt es davon noch mehr Wohnungen?
sum(df.obj_baseRent==0)
39
Ja, und zwar insgesamt 39. Der Befehl df.obj_baseRent==0 gibt einen bool’schen Array zurück, der so lang ist wie die Datenreihe obj_baseRent, und dort True ist, wo die festgelegte Bedingung wahr ist. Die Summe aller Werte des Arrays ist gleich der Anzahl von True-Werten. Haben wir bei der Warmmiete dasselbe Problem?
df.obj_totalRent.min()
0.0
sum(df.obj_totalRent==0)
63
Läuft! Bei der Warmmiete liegt der Wert noch öfter bei 0 als bei der Kaltmiete. Also behalten wir einfach alle Daten und versuchen, die extremen Ausreißer in der EDA erst einmal zu ignorieren. Schauen wir uns also die Verteilung der Kaltmieten an und ignorieren dabei jeweils die oberen und unteren 0,5% der Daten.
minimum = np.percentile(df.obj_baseRent,0.5)
maximum = np.percentile(df.obj_baseRent,99.5)
bins_und_ticks = [x for x in range(int(maximum)) if x%100==0]
kaltmiete=df.obj_baseRent.loc[df.obj_baseRent.between(minimum,maximum)]
warmmiete=df.obj_totalRent.loc[df.obj_totalRent.between(minimum,maximum)]
plt.hist(kaltmiete,bins=bins_und_ticks,alpha=0.6,color="Blue",label="Kalt")
plt.plot([kaltmiete.mean(),kaltmiete.mean()],[0,10500],color="Blue")
plt.hist(warmmiete,bins=bins_und_ticks,alpha=0.6,color="Green",label="Warm")
plt.plot([warmmiete.mean(),warmmiete.mean()],[0,10500],color="Green")
plt.annotate("Ø Kalt: "+str(int(kaltmiete.mean())), xy=(620, 9900), xytext=(1200, 10000),
arrowprops=dict(facecolor='black'))
plt.annotate("Ø Warm: "+str(int(warmmiete.mean())), xy=(810, 8400), xytext=(1200, 8500),
arrowprops=dict(facecolor='black'))
plt.xticks(bins_und_ticks,rotation=90)
plt.xlabel("Miete")
plt.ylabel("Häufigkeit")
plt.legend()
plt.show()

Das Bild zeigt zwei aufeinander liegende Histogramme. Das eine zeigt die Verteilung der Kaltmiete und das andere die Verteilung der Warmmiete. Bei mehr als 10.000 Wohnungen liegt die Kaltmiete zwischen 300€ und 400€. Logischerweise liegt die durchschnittliche Warmmiete rechts von der durchschnittlichen Kaltmiete. Hier befindet sich der Gipfel der Verteilung bei 500€ bis 600€. Doch warum ist der grüne Gipfel so viel kleiner als der blaue? Das sieht verdächtig aus. Es scheint, als würde das eine Histogramm aus viel weniger Daten bestehen als das andere. Denn wenn die beiden Histogramme jeweils ganze 99% der Wohnungen enthalten würden, dann wäre auch die Summe der einzelnen Balkenhöhen bei beiden dieselbe. Das ist jedoch nicht der Fall. Es werden anscheinend einige Daten nicht berücksichtigt. Woran liegt das?
df.obj_totalRent.count()
41103
Die Anzahl der Werte im Array obj_totalRent ist 41.103. Also sind über 11.000 Einträge leer. Für diese Wohnungen liegen keine Daten für die Warmmiete vor. Das ist zwar schade für die Analyse, aber durchaus realistisch. Ich gehe nicht von einem Fehler aus. Die leeren Einträge werden vom Histogramm einfach ignoriert. Wie sollten sie auch dargestellt werden?
Kumulierte Häufigkeiten
Ein andere (ähnliche) Möglichkeit der Visualisierung von Verteilungen ist die kumulative Verteilungsfunktion. Im Gegensatz zu Histogrammen zeigt diese Funktionen die kumulierten Häufigkeiten. Wenn der Wert einer solchen Funktion an einer bestimmten Stelle x bei y=0,5 liegt, dann ist die Hälfte der Merkmalsausprägungen der Daten kleiner oder gleich diesem bestimmten x-Wert.
kalt=df.obj_baseRent
warm=df.obj_totalRent.dropna()
sty.use("default")
farbe_kalt="deepskyblue"
farbe_warm="orangered"
percentiles = (25,75)
kalt_percentile_values=[np.percentile(kalt,x).astype(int) for x in percentiles]
warm_percentile_values=[np.percentile(warm,x).astype(int) for x in percentiles]
x_values = [np.percentile(kalt,x+1) for x in range(1,99)]
plt.step(x_values,[x/100 for x in range(1,99)],label="Kaltmiete",color=farbe_kalt)
for percentile in percentiles:
plt.plot([np.percentile(kalt,percentile),np.percentile(kalt,percentile)],
[0,1],color=farbe_kalt,linestyle="--",alpha=0.6)
x_values = [np.percentile(warm,x+1) for x in range(1,99)]
plt.step(x_values,[x/100 for x in range(1,99)],label="Warmmiete",color=farbe_warm)
for percentile in percentiles:
plt.plot([np.percentile(warm,percentile),np.percentile(warm,percentile)],
[0,1],color=farbe_warm,linestyle="--",alpha=0.6)
xtick_list=sorted(np.array([kalt_percentile_values,warm_percentile_values]).flatten().astype(int))
plt.xticks([x for x in range(0,int(max(x_values))) if x%100==0],rotation=90)
plt.yticks([x/100 for x in range(101) if x%10==0])
plt.ylim(0,1)
plt.legend()
plt.grid(alpha=0.3)
plt.fill_between(kalt_percentile_values,percentiles,color=farbe_kalt,alpha=0.2)
plt.fill_between(warm_percentile_values,percentiles,color=farbe_warm,alpha=0.2)
plt.xlabel("Miete")
plt.ylabel("Kumulierte Häufigkeit")
plt.show()

Das obige Diagramm zeigt die kumulierte Verteilung von Kalt- und Warmmieten. Zusätzlich stellt der Bereich zwischen den gestrichelten Linien die jeweils mittleren 50% der Daten dar. Die Hälfte der Wohnungen kostet zwischen 368€ und 744€ kalt und zwischen 495€ und 930€ warm. Auch können wir sagen, dass 9 von 10 Wohnungen weniger als 1100€ kalt bzw. 1300€ warm kosten. Auf dieselbe Weise können wir uns die Verteilung der Wohnungsgröße und des Baujahrs anschauen.


Das Diagramm zur Verteilung des Baujahrs sieht merkwürdig aus. Zwar ist der Graph monoton steigend, aber nicht so ebenmäßig wie die vorigen Funktionen. Den Grund dafür finden wir, wenn wir uns das zugehörige Histogramm anschauen.
df.obj_yearConstructed.hist(bins=[x for x in range(1800,2021) if x%10==0]) plt.xticks([x for x in range(1800,2021) if x%10==0],rotation=90) plt.grid(alpha=0.2) plt.show()

Im Histogramm können wir sehen, dass die Verteilung der Baujahre nicht nur einen, sondern mehrere Gipfel hat. Dadurch entstehen auch bei der kumulierten Häufigkeitsverteilung „Dellen“. Wenn die heruntergeladenen Daten repräsentativ für ganz Deutschland sind, dann können wir sagen, dass es zwei grobe Cluster von Baujahren gibt, in denen heute neu vermietete Wohnungen erbaut wurden. Ein Cluster erstreckt sich ungefähr von der Kaiserzeit bis zur Mitte des 20. Jahrhunderts, das zweite Cluster beginnt dort und endet heute. Leider haben wir nur für 7 von 10 Wohnungen Daten zum Baujahr. Darüber, wann die restlichen Immobilien gebaut wurden, kann man nur spekulieren. Erstaunlich ist zum einen der Peak in den 90er Jahren und zum anderen, wie viele Wohnung relativ neu sind. Tatsächlich befindet sich jede 15. neu vermietete Wohnung auch in einem Haus mit dem Baujahr 2017.
Sehen wir uns noch die Verteilung des Jahrs der letzten Renovierung an. Dann reicht es auch erst mal mit den kumulierten Häufigkeiten!
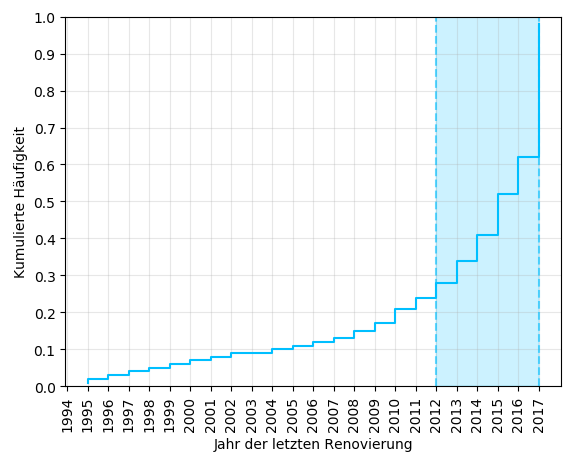
Wow, die Hälfte der Häuser wurde zum letzten Mal zwischen 2012 und 2017 renoviert. Richtig? Nicht ganz. Denn bei über 70% aller Wohnungen gibt es zum Jahr der letzten Renovierung keine Daten. Diesen Umstand sind wir beim Erstellen des Diagramms jedoch gekonnt umgangen. Also können wir nur mit Sicherheit sagen, dass mindestens 15% der Wohnungen zwischen 2012 und 2017 renoviert wurden. Die Wohnungen, zu denen die Daten fehlen, wurden möglicherweise noch kein einziges Mal renoviert. Mit verallgemeinernden Aussagen sollte man also – wie so oft – vorsichtig sein.
Die ersten Schritte sind getan
Wir haben uns jetzt einen ersten Überblick über die Daten verschafft und mehrere Möglichkeiten zur Visualisierung von Verteilungen kennengelernt. Im nächsten Artikel werden wir unter anderem ich auf die Unterschiede zwischen den Wohnungen der einzelnen Bundesländer eingehen und mit Boxplots eine weitere Möglichkeit zur grafischen Darstellung von Verteilungen ins Spiel bringen.

