Mit linearer Regression überprüfst du ganz einfach, ob es zwischen zwei Merkmalen einen linearen Zusammenhang gibt. Wie genau du das anstellst, erfährst du hier.

Ein einführendes Beispiel

Wenn du schon weißt, was lineare Regression ist, kannst diesen und den Theorieteil ignorieren und direkt zur Implementierung in Python springen. Allerdings wird das Beispiel auch dort benutzt.

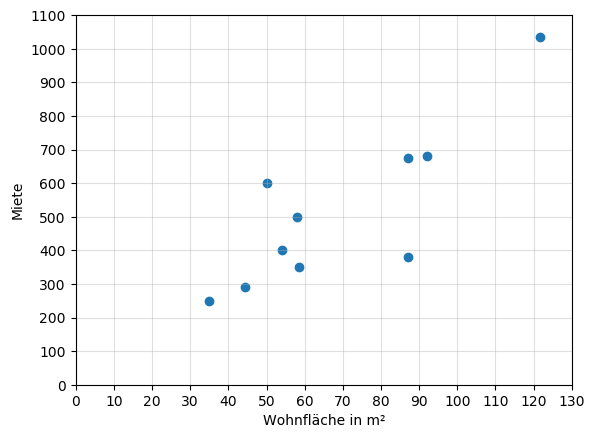
Stell dir vor, du willst umziehen. Du bist gerade auf Wohnungssuche und weißt noch nicht, wie viel dich deine neue Wohnung kosten wird. Allerdings willst du nicht einfach in die Wohnung mit der geringsten Miete ziehen, sondern du hast Ansprüche – vor allem an die Wohnfläche. Mindestens 60 Quadratmeter sollten es sein. Doch wie viel musst du schätzungsweise für eine Wohnung in der Größe bezahlen? Um die Frage zu klären, siehst du dir im Internet einige Wohnungen samt Wohnfläche und Miete an. Dass größere Wohnungen tendenziell teurer als kleinere sind, weißt du schon aus Erfahrung. Um die Aussage zu überprüfen, zeichnest du die Miete und Quadratmeterzahl jeder Wohnung auf. Dabei siehst du folgendes.

Das Bild stimmt mit deiner Erfahrung überein, es existiert – zumindest in deiner Stichprobe – ein positiver Zusammenhang zwischen Wohnfläche und Miete. Trotzdem ist die aus den Daten gewonnene Aussage ein wenig schwammig. Manche der Wohnungen kosten dasselbe, aber unterscheiden sich enorm in der Wohnfläche. Du willst eine einheitliche Regel finden, mit der du genau schätzen kannst, wie viel du für eine Wohnung mit 60m² ausgeben musst. Und genau dabei hilft dir lineare Regression.

Was ist lineare Regression?

Lineare Regression ist ein statistisches Verfahren, mit dessen Hilfe eine Gerade auf die Weise durch die Daten gelegt wird, dass sie die Daten am besten repräsentiert. Und das ist genau dann der Fall, wenn die Summe der quadrierten Abstände zwischen der Geraden und den Daten am kleinsten ist. Diese Methode zur Bestimmung der Gerade nennt man auch die Methode der kleinsten Quadrate. Mit diesem Schätzer erhältst du eine Funktion, mit deren Hilfe du für jeden Wert einer unabhängigen Variable (Wohnfläche) den Wert der abhängigen Variable (Miete) bestimmen kannst.

Die Gerade ist definiert durch die Gleichung ist y=a+b*x. Die Miete im Beispiel wird hier durch die Zielgröße y repräsentiert. Unser Ziel ist es, y für jede beliebige Quadratmeterzahl zu berechnen. Das tun wir mit Hilfe der unabhängigen Variable x, dem Achsenabschnitt a und dem Steigungskoeffizienten b. Was die unabhängige Variable ist, haben wir bereits geklärt. Der Achsenabschnitt ist der Wert von y, bei dem die Gerade die senkrechte Achse schneidet. In unserem Beispiel wäre das theoretisch die Miete, welche man für eine Wohnung mit 0 Quadratmetern zahlen müsste. Der Koeffizient b ist der Wert, mit dem die Zielgröße ansteigt, wenn man die unabhängige Variable mit 1 erhöht. Auf unser Beispiel bezogen: Wie viel mehr muss ich für eine Wohnung bezahlen, die einen Quadratmeter größer ist? Die genaue Herleitung der gesamten Geradengleichung kannst du bei crashkurs-statistik.de nachlesen.

Implementierung in Python

Um ein lineares Regressionsmodell in Python umzusetzen, brauchst du nur wenige Arbeitsschritte. Die Basis bildet die Funktion linregress des Python-Packages Scipy. Dieses Package bietet allerlei Werkzeuge für Statistik und ist unter anderem Bestandteil der Anaconda-Distribution. Solltest du noch nicht im Besitz von Scipy sein, kannst du hier nachschauen, wie du es installierst.

from scipy.stats import linregress

Scipy hat eine eigene Funktion für lineare Regressionsanalyse. Als Argumente weist man ihr jeweils einen Array der x– und der y-Werte zu. Neben Numpy-Arrays akzeptiert die Funktion auch Listen, Tupel und Pandas Series. Als Ergebnis erhalten wir dann die Steigung, den Achsenabschnitt, den Korrelationskoeffizienten nach Pearson (R), den p-Wert und die Standardabweichung. Die einzelnen Werte kann man in dieser Reihenfolge auch gleich beim Aufrufen der Funktion in separate Objekte entpacken. So kann man anschließend besser mit den Kennzahlen arbeiten.

b, a, r, p, std = linregress(wohnflaeche,miete)

Folgende Werte wurden von der Funktion ausgerechnet.

b = 7,37
a = 8,96
r = 0,83
p = 0,00
std = 1,72

Damit lautet unsere Geradengleichung:

y = 8,96 + 7,37 * x

oder 

Miete = 8,96 + 7,37 * Wohnfläche

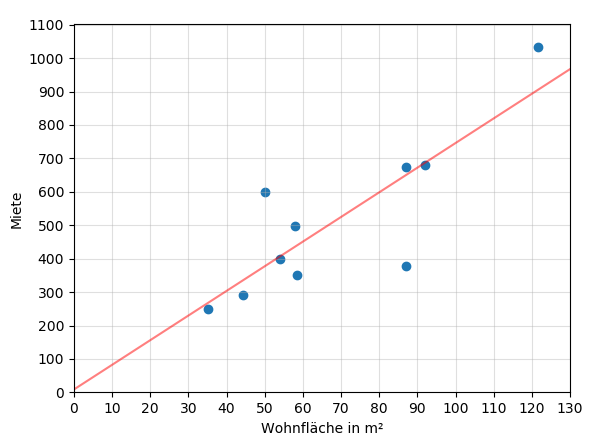
Was bedeuten die Werte für unser Beispiel? Ein Wert von 8,96 für den Achsenabschnitt bedeutet, dass laut dem Modell eine Wohnung mit 0 Quadratmetern Wohnfläche 8,96€ im Monat kostet und mit jedem Quadratmeter 7,37€ teurer wird. Mit der Wohnfläche steigt die geschätzte Miete linear an, deshalb auch lineare Regression. Jetzt können wir ausrechnen, wie viel wir für eine 60m² große Wohnung zahlen müssen – und zwar 451,16€. Die Regressionsgerade lässt sich auch ganz einfach zusammen mit dem oben gezeigten Streudiagramm darstellen.

plt.scatter(wohnflaeche, miete)
plt.plot([0,130],[a,a+130*b],c="red",alpha=0.5)
plt.plot()

plt.xlim(0,130)
plt.ylim(0,1100)

plt.xlabel("Wohnfläche in m²")
plt.ylabel("Miete")
plt.grid(alpha=0.4)
plt.xticks([x for x in range(131) if x%10==0])
plt.yticks([x for x in range(1101) if x%100==0])

plt.show()

Natürlich ist es nur in einem gewissen Rahmen sinnvoll, die Miete in Abhängigkeit von der Wohnfläche zu schätzen. In der Realität wirst du wohl kaum 10m² große Wohnungen finden. Doch für den Bereich, in dem uns Daten vorliegen, scheint die lineare Regression eine recht gute Annäherung zu sein.

Vor- und Nachteile von linearer Regression

In der Gesamtmenge von statistischen Modellen und Machine-Learning-Algorithmen gehört lineare Regression zu den Basics. Die Methode ist leicht zu verstehen und einfach zu interpretieren. Vor allem bei großen Datenmengen kommt der Vorteil hinzu, dass diese Methode im Vergleich zu anderen Verfahren einem Computer relativ wenig Rechenleistung abverlangt. Am anderen Ende des Spektrums haben wir beispielsweise neuronale Netze, die – abhängig von der Komplexität und Datenmenge – mehrere Tage brauchen können, bis sie sich an die Daten „optimal“ angepasst haben.

Der Nachteil linearer Regressionsmodelle ist, dass sie oft ungenauer sind als komplexere Methoden. Zwar wird auch heute noch oft lineare Regression eingesetzt (aus den oben genannten Gründen), in vielen praktischen Anwendungen wird heutzutage jedoch auf andere Verfahren zurückgegriffen. Hauptgrund für die Entwicklung hin zu komplexeren Modellen ist die enorm gewachsene Rechenleistung in den letzten 10 Jahren und die damit verbundenen geringeren Kosten für rechenintensive Verfahren.