Mensch ärgere Dich nicht! Eine Würfel-Simulation in Python
Wie oft musst du im Durchschnitt würfeln, um deine Figur ins Spiel zu bringen? Eine kleine Simulation in Python verrät es dir.
Die kurze Antwort: 6-mal. Klar, ein Würfel hat 6 Seiten und die Wahrscheinlichkeit, eine 6 zu würfeln, beträgt 1/6. Aber wer braucht schon Wahrscheinlichkeitsrechnung, wenn man den Kram einfach simulieren kann? So können wir auch untersuchen, mit welcher Wahrscheinlichkeit wir 2,3 oder 10 Würfe brauchen, um unsere Figur auf das Spielfeld zu befördern.
(Disclaimer: Häufigkeiten und Wahrscheinlichkeiten werden hier wild durcheinander geworfen, obwohl die Begriffe streng genommen nicht identisch sind.)
Simulation in Python
Der Code für die Simulation sieht so aus.
import numpy as np
versuche_liste=[]
for i in range(100000):
versuche = 0
wurf = 0
while wurf != 6:
versuche+=1
wurf = np.random.choice([1,2,3,4,5,6])
versuche_liste.append(versuche)
Als erstes definieren wir eine leere Liste, in die wir später für jeden Durchgang die Anzahl der Versuche bis zur ersten 6 hinein schreiben. Dann werden 100.000 Spiele simuliert, bei denen jeweils so lange gewürfelt wird, bis die erste 6 kommt. Solang keine 6 kommt, steigt die Anzahl der Versuche um 1. Das Endergebnis pro Runde wird dann in die oben erwähnte Liste geschrieben.
Die Verteilung der Endergebnisse sieht dann so aus.
import matplotlib.pyplot as plt
plt.hist(versuche_liste,
bins=[x for x in range(1,max(versuche_liste))],
normed=True)
plt.xlabel("Anzahl Versuche")
plt.ylabel("Relative Häufigkeit")
plt.grid(alpha=0.2)
plt.show()

Oben im Histogramm siehst du, wie oft nach einer bestimmten Anzahl von Würfen die 6 gewürfelt wurde. Die größte Einzelwahrscheinlichkeit liegt mit 16,6% tatsächlich bei einem Versuch. Das bedeutet natürlich auch, dass in 83,4% der Fälle mehr als ein Wurf gebraucht wurde.
Die genauen Wahrscheinlichkeiten siehst du hier.
import pandas as pd
df = pd.DataFrame({"versuche":versuche_liste})
df.versuche.value_counts(normalize=True)[:20]
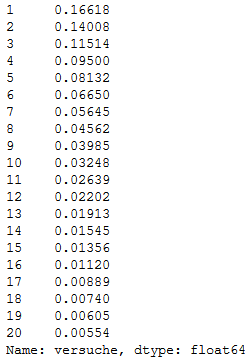
Solltest du also 10 Würfe brauchen, um ins Spiel zu kommen, dann hast du wirklich großes Pech. Die Wahrscheinlichkeit dafür liegt nämlich bei 3,248%.
So viel zu den Einzelwahrscheinlichkeiten. Wenn wir wissen wollen, mit welcher Wahrscheinlichkeit man weniger oder mehr als X Versuche für eine 6 braucht, muss man sich die kumulierten Wahrscheinlichkeiten anschauen. Diese wiederum sehen so aus.
plt.hist(versuche_liste,
bins=[x for x in range(1,max(versuche_liste))],
normed=True,
cumulative=True)
plt.xlabel("Anzahl Versuche")
plt.ylabel("Kumulierte Häufigkeit")
plt.grid(alpha=0.2)
plt.show()

Das Diagramm zeigt, wie hoch die Wahrscheinlichkeit dafür ist, dass man maximal X-mal würfeln muss, bis eine 6 kommt. Die Gegenwahrscheinlichkeit ist somit die Wahrscheinlichkeit, mit der man mehr als X Versuche braucht, bis man eine 6 würfelt. Unten siehst du noch mal die genauen Wahrscheinlichkeiten.
for i in range(1,21):
print("Anzahl Versuche<="+str(i)+": "
+str(round((df.versuche <=i).mean(),3))
+" | Anzahl der Versuche>"+str(i)
+": "
+str(round((df.versuche >i).mean(),3)))

Das war sie auch schon, die kleine Simulation eines Teils von „Mensch ärgere dich nicht!“. Viel Spaß beim Nachmachen! Für eine kleine Challenge kannst du auch versuchen, die Ergebnisse nicht in einem Histogramm, sondern mit einem Boxplot zu visualisieren. Was Boxplots sind und welche weiteren Möglichkeiten zur Darstellung es gibt, erfährst du in dieser Beitragsreihe.

