Wie viele unterschiedliche Kartenkombinationen gibt es beim Poker? 2,6 Millionen. Und wie viele davon muss man einem neuronalen Netz zeigen, damit es deren Ranking lernt? Ein Hundertstel. Mehr dazu erfährst du in diesem Beitrag.

Wer kennt das nicht?

Man will in Python einen Poker Bot bauen, um endlich auf bequeme Art und Weise im Internet reich zu werden. Und dann fällt einem auf, dass der Bot zuallererst einmal wissen muss, wie gut ein gegebenes Blatt überhaupt ist. Eine mögliche Lösung des Problems ist die Definition von formalen Regeln nach dem Schema „Sind Karte 1 und Karte 2 beide eine 4, dann ist es ein Pärchen“. Doch dann fragst du dich, wie viele mögliche Kombinationen von Pokerhänden es eigentlich gibt.

Für kombinatorische Funktionen gibt es das nette Python-Modul itertools. Unter anderem können wir damit das Ziehen von 5 Karten aus insgesamt 52 Karten ohne Beachten der Reihenfolge und ohne Zurücklegen simulieren.

from itertools import combinations

len([komb for komb in combinations(
    [karte for karte in range(52)],5)])

#=2598960

Es gibt also knapp 2,6 Millionen verschiedene Pokerhände. Natürlich kannst du durch langes scharfes Nachdenken formale Regeln definieren und jeder Kombination von Karten einen korrekten Rang zuordnen. Du willst aber nicht lange überlegen. Außerdem hast du letztens dein erstes neuronales Netz gebaut und denkst, dass neuronale Netze der Hammer sind und sowieso mittlerweile fast alles können. Doch auch einem neuronalen Netz musst du Daten bereitstellen, anhand derer es lernen kann.

Zum Glück gibt es diesen Poker-Datensatz des UCI Machine Learning Repository, der 25.000 bzw. 1.000.000  Hände inklusive des jeweiligen Rankings enthält. Im Data Folder befinden sich sowohl ein Trainings- als auch ein Testdatensatz. Beide habe ich heruntergeladen und als CSV-Datei abgespeichert (wichtig für die weitere Bearbeitung in Python).  In 10 Spalten stehen sowohl die Ränge (2 bis Ass) als auch die Farben (Herz, Karo, Pik, Kreuz) der jeweiligen Karten. Die letzte Spalte beinhaltet Zahlen von 0 bis 9, welche das Ranking der kompletten Hand widerspiegeln.

0: Keine zueinander passenden Karten
1: Ein Pärchen 
2: Zwei Pärchen 
3: Drillinge 
4: Straight
5: Flush
6: Full house
7: Vierlinge 
8: Straight flush 
9: Royal flush

Schauen wir uns die Daten mal an.

Trainings- und Testdaten einlesen

Laden wir mal die Trainings- und Testdaten in Python und werfen einen Blick drauf.

import pandas as pd

train = pd.read_csv("...\poker-hand-training-true.csv",
                    header=None,
                    names=["S1","C1","S2","C2","S3","C3","S4","C4","S5","C5","hand"])
train.sample(10)

train.shape

test = pd.read_csv("...\poker-hand-testing.csv",
                    header=None,
                    names=["S1","C1","S2","C2","S3","C3","S4","C4","S5","C5","hand"])
test.sample(10

test.shape

Die Spaltennamen habe ich analog zur Seite der UCI vergeben, wobei „S1“ die Farbe und „C1“ der Rang der ersten gezogenen Karte ist. Nehmen wir als Beispiel die dritte Zeile von oben. Die erste Karte ist ein Karo Ass, die zweite Karte eine Kreuz 9, die dritte Karte eine Herz 9, die vierte Karte eine Karo 9 und die fünfte Karte eine Kreuz 4. Insgesamt halt wir in dieser Zeile einen Drilling auf der Hand, womit die Pokerhand einen Wert von 3 besitzt. Die Verteilung der Hände sieht wie folgt aus.

train.hand.value_counts(normalize=True)

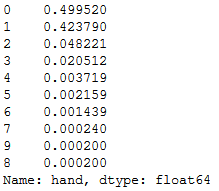
train.hand.value_counts(normalize=True).plot(kind="bar")
plt.xlabel("Hand")
plt.ylabel("Relative Häufigkeit")
plt.show()

Die Verteilung der Hände stimmt mit der echten Wahrscheinlichkeitsverteilung laut Wikipedia weitestgehend überein. Auffällig ist nur, dass im Datensatz genauso viele Vierlinge wie Royal Flushs vorkommen, obwohl ein Vierling ca. 15 mal wahrscheinlicher als ein Royal Flush ist. Doch das soll nicht das Problem sein. Was schon eher ein Problem darstellen kann, ist die extreme Ungleichverteilung der Häufigkeiten. Kann ein Algorithmus lernen, was ein Royal Flush ist, wenn dieser nur in 0,02% der Fälle vorkommt? Wir werden sehen.

Die Daten vorbereiten

Der erste Schritt der Vorbereitung ist die Umwandlung der Daten in (Numpy-)Arrays. Hierbei besteht die Variable X aus den 10 oben genannten Spalten mit den Karteneigenschaften und y ist die Spalte mit dem Ranking der jeweiligen Hand.

X = train.drop("hand",axis=1).values
y = train.hand.values

Die Zielvariable y befindet sich allerdings noch nicht im richtigen Format. Wir müssen sie in eine Matrix aus Dummy-Variablen umwandeln, welche nur aus Nullen und Einsen besteht. Was bedeutet das genau? Momentan haben wir eine Spalte mit Zahlen von 0 bis 9. Damit können wir das neuronale Netz nicht sinnvoll trainieren. Aus dieser einen Spalte machen wir deshalb 10 Spalten – eine für Pärchen, eine für Drillinge und so weiter. Liegt dann wirklich ein Drilling vor, dann ist der Eintrag in der Spalte für Drillinge 1, während alle anderen Spalten 0 bleiben.

dummy_y = np_utils.to_categorical(y)
print(dummy_y[:20])

Zum Beispiel steht in der ersten Zeile des neuen Arrays in der zehnten Spalte eine 1. Das ist die Spalte, welche 1 wird, sofern die dazugehörige Hand ein Royal Flush ist. Dies ist hier der Fall. In der untersten Zeile sehen wir hingegen in der zweiten Spalte eine 1, die Hand ist also ein Pärchen.

Jetzt haben wir die Trainingsdaten so formatiert, dass wir sie dem Algorithmus vorwerfen können. Als nächstes bauen wir das Modell und trainieren es.

Neuronales Netz mit Keras bauen

Auch hier importieren wir zuerst alle benötigten Funktionen.

from keras.models import Sequential
from keras.layers import Dense

Wir bauen mit der Deep-Learning-Bibliothek Keras ein ganz normales neuronales Netz (engl.: Deep Neural Network), bei dem alle Knoten einer Schicht mit allen Knoten der vorigen bzw. folgenden Schicht verbunden sind.

model = Sequential()
model.add(Dense(52, input_dim=X.shape[1], kernel_initializer='normal', activation='relu'))
model.add(Dense(52, kernel_initializer='normal', activation='relu'))
model.add(Dense(10,activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

Die Funktion Sequential() erlaubt uns, manuell Schicht für Schicht zum Modell hinzuzufügen. Hierbei können wir jede Schicht einzeln konfigurieren. In der ersten Schicht müssen wir dem Modell mitteilen, welche Dimensionen die Inputvariable hat. Da wir dem Modell einen Array mit 10 Spalten übergeben, ist das auch die Zahl, welche wir dem Argument input_dim zuweisen. Ingesamt haben wir ein neuronales Netz mit 3 Schichten, von denen die letzte die sogenannte Output-Schicht ist. In dieser Schicht gibt das Modell für jedes Blatt die Wahrscheinlichkeiten zurück, mit denen es sich bei den gegebenen Karten um ein Pärchen, Drilling, Vierling und so weiter handelt.

Na dann lass uns das Modell trainieren. Entweder so:

model.fit(X, dummy_y, epochs=200, batch_size=25)

Oder so:

hist = model.fit(X, dummy_y, epochs=200, batch_size=25)

In beiden Fällen wird das neuronale Netz trainiert, im zweiten Fall werden aber die Modellparameter in die Variable hist geschrieben, unter anderem auch die Entwicklung verschiedener Messwerte im Trainingsverlauf. Standardmäßig wird schon während des Trainings ein Verlauf ausgegeben.

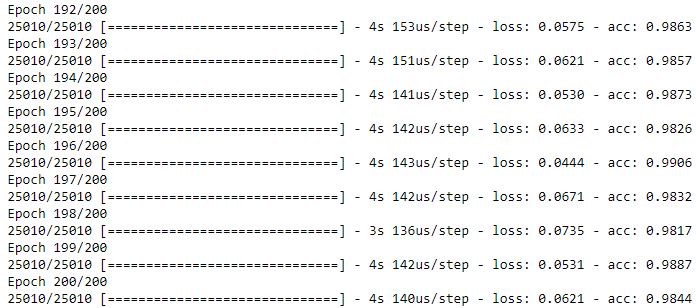
Nach 200 Epochs haben wir einen Accuracy Score von 98% erreicht. In 98 von 100 Fällen schätzt das Modell die Güte der vorliegenden Pokerhand also richtig ein. Sehen wir uns noch die Historie des Scores an.

plt.plot(hist.history["acc"])
plt.xlabel("Epoch")
plt.ylabel("Accuracy")
plt.title("Modellperformance")

plt.show()

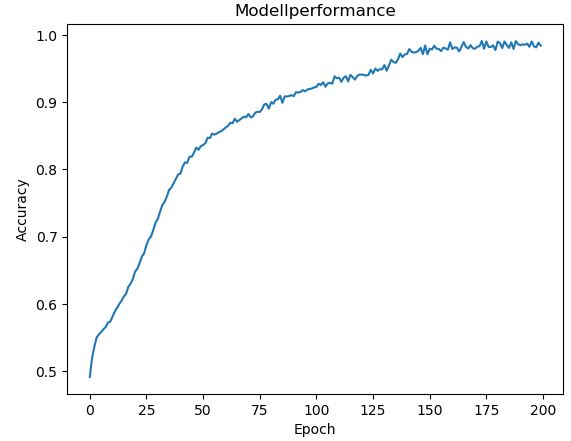
Wie wir sehen, beginnt der Accuracy Score schon auf einem relativ hohen Niveau. Das ist dadurch zu erklären, dass selbst ein Schätzer, der bei jeder Pokerhand eine Null zurückgibt, in 50% der Fälle richtig liegt – siehe Balkendiagramm oben. Der Score steigt bis Epoch 150 relativ schnell an. Dann verlangsamt sich das Wachstum, bis der Score nach 200 Epochs schließlich 98% erreicht.

Das neuronale Netz testen

Dieser Score oben bezieht sich ausschließlich auf die Trainingsdaten. Ziel des Modells ist aber, neue Daten richtig einzuschätzen. Und da neuronale Netze besonders zu Overfitting (eine zu starke Anpassung des Modells an die Trainingsdaten und damit schlechte Performance bei neuen Daten) neigen, müssen wir die Güte des Modells anhand neuer Daten prüfen. Darum evaluieren wird jetzt das Modell Testdaten. Doch zuerst schauen wir uns auch hier noch kurz die Verteilung der Hände an.

test.hand.value_counts(normalize=True).plot(kind="bar")
plt.xlabel("Hand")
plt.ylabel("Relative Häufigkeit")
plt.show()

test.hand.value_counts(normalize=True)

Sieht fast genau so aus wie die Verteilung der Hände in den Testdaten. Schauen wir mal, ob das Modell von den gut 25.000 Pokerhänden so gut abstrahiert hat, dass es auch die eine Million Blätter des Testdatensatzes richtig einschätzt. Analog zu oben müssen wir auch hier X und y ins richtige Format bringen.

X_test = test.drop("hand",axis=1).values
y_test = test.hand.values
dummy_y_test = np_utils.to_categorical(y_test)

Jetzt wird es spannend!

model.evaluate(X_test,dummy_y_test)

Auch bei den Testdaten performt das Modell mit einem Score von 99% ziemlich gut. Doch um auf das Problem von oben zurück zu kommen: Erkennt es auch zuverlässig Royal Flushs? Diese kommen im Testdatensatz nur dreimal vor. Selbst wenn das neuronale Netz keinen einzigen Royal Flush richtig erkennt, kann sein Accuracy Score trotzdem noch weit über 99% liegen. Finden wir es heraus und zeigen dem Modell vier verschiedene von uns generierte Royal Flushs.

print("Herz: Ass, König, Dame, Bube, 10\n"+str(
    np.round(
        model.predict(
            np.array(
                [[1,1,1,13,1,12,1,11,1,10]])).flatten(),2)))

print("Pik: Ass, König, Dame, Bube, 10\n"+str(
    np.round(
        model.predict(
            np.array(
                [[2,1,2,13,2,12,2,11,2,10]])).flatten(),2)))

print("Karo: Ass, König, Dame, Bube, 10\n"+str(
    np.round(
        model.predict(
            np.array(
                [[3,1,3,13,3,12,3,11,3,10]])).flatten(),2)))

print("Kreuz: Ass, König, Dame, Bube, 10\n"+str(
    np.round(
        model.predict(
            np.array(
                [[4,1,4,13,4,12,4,11,4,10]])).flatten(),2)))

Bei einem Royal Flush ist das neuronale Netz sich also zu 100% sicher, dass wir nichts auf der Hand halten. Dazu muss man natürlich sagen, dass der Algorithmus extrem wenige Beispiele für Royal Flushs gesehen hat. Vielleicht könnte man das Problem beheben, indem man in die Trainingsdaten noch mehr Beispiele für diese Art von Hand einpflegt. Immerhin gibt es unter Berücksichtigung der Kartenreihenfolge 480 Möglichkeiten, einen Royal Flush zu ziehen. Generell wäre es jetzt interessant zu wissen, bei welchen Pokerhänden sich das Modell sicher oder unsicher ist und ob es sicher die korrekte oder falsche Antwort gibt.

Bei welchen Händen ist das Modell sich sicher?

Dafür lassen wir die predict()-Methode des Modells noch mal über die gesamten Testdaten laufen und weisen den geschätzten Wahrscheinlichkeiten eigene Spalten zu.

test2 = test

pred = model.predict(test.drop("hand",axis=1).values).T

test2["high_card"] = pred[0]
test2["paerchen"] = pred[1]
test2["zwei_paerchen"] = pred[2]
test2["drillinge"] = pred[3]
test2["straight"] = pred[4]
test2["flush"] = pred[5]
test2["full_house"] = pred[6]
test2["vierlinge"] = pred[7]
test2["straight_flush"] = pred[8]
test2["royal_flush"] = pred[9]

Die neuen Spalten sehen dann so aus.

round(test2.head(),2)

Links siehst du immer noch die einzeln Karten und in der Mitte das Ranking der gesamten Hand. Auf der rechten Seite siehst du nun für jede mögliche Pokerhand, für wie wahrscheinlich der Algorithmus diese Hand hält – gegeben die Karten, die wir ihm zeigen. Uns interessiert aber nicht jedes einzelne Blatt. Wir wollen für jede Art von Hand sehen, wie sicher sich der Algorithmus dort ist. Dafür gruppieren wir die Tabelle nach der Spalte hand und berechnen für alle anderen Spalten den Durchschnittswert.

group = test2.groupby("hand").agg({"high_card":["mean"],
                                   "paerchen":["mean"],
                                   "zwei_paerchen":["mean"],
                                   "drillinge":["mean"],
                                   "straight":["mean"],
                                   "flush":["mean"],
                                   "full_house":["mean"],
                                   "vierlinge":["mean"],
                                   "straight_flush":["mean"],
                                   "royal_flush":["mean"]})
group.index = ["high_card",
               "paerchen",
               "zwei_paerchen",
               "drillinge",
               "straight",
               "flush",
               "full_house",
               "vierlinge",
               "straight_flush",
               "royal_flush"]

group.columns = group.columns.get_level_values(0)

round(group,2)

Die Tabelle oben zeigt, dass wenn wir dem Algorithmus beispielsweise ein Pärchen zeigen, dass er sich im Schnitt zu 99% sicher ist, dass das Blatt auch wirklich ein Pärchen enthält. Unten siehst du dazu eine Heatmap, damit die Ergebnisse mehr ins Auge fallen.

import seaborn as sns

sns.heatmap(round(group,2),annot=True)
plt.ylabel("Echte Hand")
plt.xlabel("Geschätzte Hand")
plt.show()

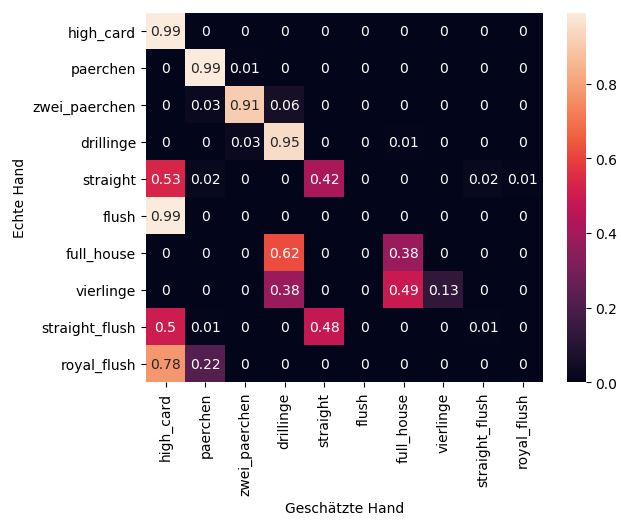
Die vertikale Achse stellt hier die echten Hände dar, während auf der horizontalen Achse die prognostizierten Hände stehen. Von High Card bis Drilling sieht alles recht stabil aus. Bei der Straße ist das neuronale Netz sich schon ziemlich unsicher, ob wir nicht doch einfach gar nichts auf der Hand haben. Beim Flush ist das Modell sich wieder sehr sicher, liegt allerdings grandios falsch. Der Algorithmus scheint den Zusammenhang zwischen Karten mit derselben Farbe nicht wirklich zu verstehen. Bei einem Full House schwankt das neuronale Netz zwischen einem Drilling und einem Full House, wobei der Drilling leider favorisiert wird. Bei den drei besten Blättern kommt das Modell komplett durcheinander.  Tendenziell kann man sagen: Je höher das Blatt, desto schlechter die Schätzung. Allerdings machen die vier schlechtesten Pokerhände (High Card, Pärchen, Zwei Pärchen, Drillinge) schon 99,24% aller möglichen Kartenkombinationen aus. Das heißt, wenn der Algorithmus dort richtig prognostiziert, ist er schon mal sehr präzise.

Fazit

Wir haben ein simples neuronales Netz gebaut, welches in 99% der Fälle einer Kombination aus 5 Pokerkarten das richtige Ranking zuweisen kann. Allerdings wird die Vorhersagekraft des Schätzer schlechter, je besser das Blatt wird. Bestimmt kann man einen präziseren Schätzer bauen, wenn man das Modell verbessert. Was denkst du, wie kann man das Modell verbessern? Lade dir einfach selbst die Daten herunter und spiele ein bisschen mit den Modellparametern und mit der Breite/Tiefe des Modells. Vielleicht muss das Modell länger trainiert werden, vielleicht muss man weitere Schichten hinzufügen und so weiter. Ich freue mich auf Vorschläge!